Conchoid of Nicomedes
History
According to common modern accounts, the conchoid of Nicomedes was first conceived around 200 B.C by Nicomedes, to solve the angle trisection problem. The name conchoid is derived from Greek meaning “shell”, as in the word conch. The curve is also known as cochloid.
From E. H. Lockwood (1961): The invention of the conchoid (‘mussel-shell shaped’) is ascribed to Nicomedes (second century B.C.) by Pappus and other classical authors; it was a favourite with the mathematicians of the seventeenth century as a specimen for the new method of analytical geometry and calculus. It could be used (as was the purpose of its invention) to solve the two problems of doubling the cube and of trisecting a angle; and hence for veery cubic or quartic prblem. For this reason, Newton suggested that it would be treated as a 'standard' curve.
Did Nicomedes use the curve to double the cube? Who used the name cochloid and in where?
Description
Conchoid of Nicomedes describes a family of curves of one parameter. They are special cases of the general conchoid. They are the conchoids of a line.
Step-by-step explaination:
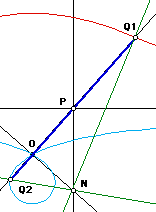
- Given a line l, a point O not on l, and a distance k.
- Draw a line m passing O and any point P on l.
- Mark points Q1 and Q2 on m such that distance[Q1,P]==distance[Q2,p]==k.
- The locus of Q1 and Q2 for variable point P on l is the conchoid of Nicomedes.
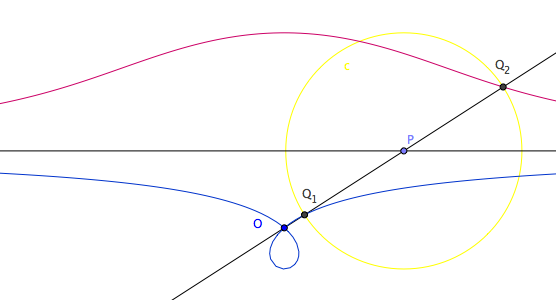
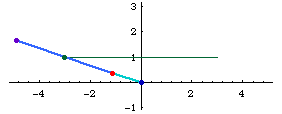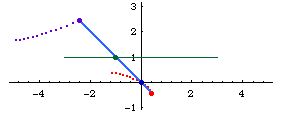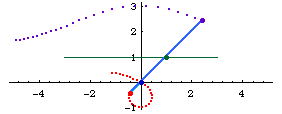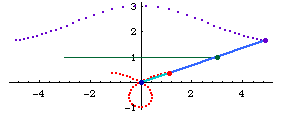
The point O is called the pole. The given line is called its directrix, and is a asymptote.
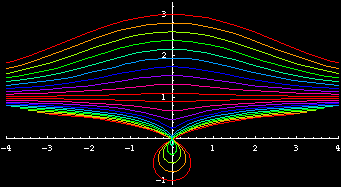
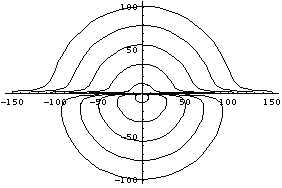
Formula
Let the distance between pole and line be b, and the given constant be k. The curve only has one parameter k, because for a given b, all families of the curve can be generated by varing k (they only differ in scale). (similarly, we can use b as the parameter.) In a mathematical context, we shoud just use b==1. However, it is convenient to have formula that have both b and k. Also, for a given k, the curve has two branches. In a math context, it would be better to define the curve with a signed constant k corresponding to a curve of only one branch. We will be using this intepretation of k. In this respect, the conchoid of Nichomedes is then two conchoids of a line with constants k and -k.
The curve with negative offset can be classified into three types: if b < k there is a loop; if b == k, a cusp; and if b > k, smooth. Curves with positive offsets are always smooth.
The following formulas are for conchoid of a line y==b, pole O at the origin, and offset k.
Polar: r==b/Sin[θ]+k, -Pi/2 < θ < Pi/2. This equation is easily derived. Because a line x==b in polar equation is r==b/Cos[θ] with -Pi/2 < θ < Pi/2.
Some observation of Cosine shows that if θ goes from 0 to 2 Pi, two conchoids with offset ±Abs[k] results from a single equation r==b/Cos[θ]+k. To rotate the graph by Pi/2, we replace cosine by sine.
Parametric: {t + (k*t)/Sqrt[b^2 + t^2], b + (b*k)/Sqrt[b^2 + t^2]}, -Infinity < t < Infinity.
This equation follows from the parametric formula for the general conchoid, where the general point {x,y} is replaced by the curve of a line {t,b}, and pole {a,b} is replaced by {0,0}.
If we substitute t in the above parametric equation by b*Tan[t], we have this form: (k + b/Cos[t])*{Sin[t],Cos[t]}, -Pi/2 < t < 3/2 Pi. t ≠ Pi/2. This form is a direct translation from the polar formula.
For conchoids of a line with positive and negative offsets k and a point at origin, the Cartesian equation is: (x^2+y^2)*(y-b)^2==k^2*y^2. If k < b, the point at origin is a isolated point.
if k < 0 and b < Abs[k], the conchoid has a loop with area (b*Sqrt[k^2-b^2]-2*b*k*Log[(k+Sqrt[k^2-b^2])/b]+k^2*ArcCos[b/k]). The area between any conchoid of a line and its asymptote is infinite. need proof.
From Lockwood: “The gradient at the node is given by Cos[psi]==+-b/k”. Not sure what it means.
Properties
Tangent Construction
Look at the conchoid tracing as a mechanical device, where a bar line[O,P] slides on a line at P and a fixed joint O. The point P on the bar moves along the directrix, and the point at O moves in the direction of vector[O,P]. We know the direction of motion of the bar at the two joins O and P at any time. The intersection of normals to these directions forms the instaneous center of rotation N. Since the tracing points Q1 and Q2 are parts of the apparatus, thus N is also their center of rotation and therefore line[N,Q1] and line[N,Q2] are the curve's normals.
Angle Trisection
- The curve can be used to solve the Greek Angle Trisection problem.
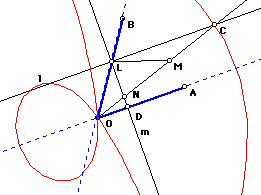
- Given a acute angle AOB, we want to construct a angle that is 1/3 of AOB, with the help of conchoid of Nicomedes.
- Steps: Draw a line m passing segment[A,O] and perpendicular to it.
- Let D:=intersection[m,line[A,O]], L:=intersection[m,line[B,O]].
- Suppose we are given a conchoid of Nicomedes, with pole at O, line m, and offset 2*distance[O,L].
- Draw line l passing L and perpendicular to m.
- Let C be a intersection of the curve and l, the one on the opposite side of the pole.
- angle[A,O,B]==3*angle[A,O,C].
- Proof:
- angle[A,O,C]==angle[O,C,L] since line[O,C] cuts parallel lines.
- Let q:=line[O,C], N:=intersection[m,q], M:=midpoint[N,C], k:=distance[O,L].
- By our construction, we have distance[N,M]==distance[M,C]==k.
- Since NLC is a right triangle, we see that MN, ML, MC, OL all have the same length, thus triangle[M,L,C] and triangle[M,L,N] are isosceles and it follows that angle[N,M,L]==2*angle[M,C,L].
- Since distance[O,L]==distance[M,L], triangle[M,L,O] is also a isosceles, and thus two of its angles are equal.
- We have shown that angles equivalent to angle[A,O,C] is 1/3 times angles equivalent to angle[A,O,B].
- End of proof.
The essential element where the conchoid made the trisection possible is the construction of the point C on l such that distance[N,C]==2*distance[O,L], where N is the intersection of m and line[O,C]. Note that for each angle to trisect, a new conchoid is needed. This is in contrast to some other trisectrixes such as the quadratrix, where all angles can be trisected once the curve is given.
Doubling the Cube
The curve can be used to solve the Greek Cube Doubling problem.
How to use this curve to double the cube?
Graphics Gallery
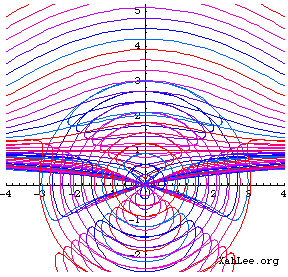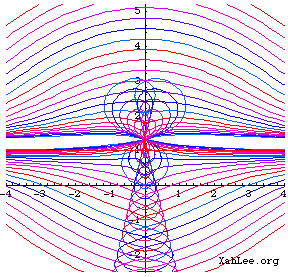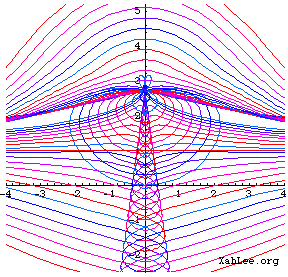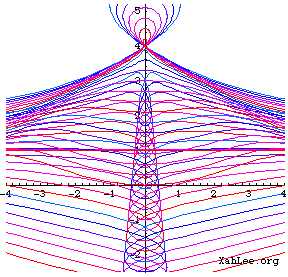
Related Web Sites
- Mathematica Packages for Plane Curves
- Curves and Their Properties: Conchoid, p031
- https://mathshistory.st-andrews.ac.uk/Curves/Conchoid/
- Szmulowicz, F. Conchoid of Nicomedes from Reflections and Refractions in a Cone. Amer. J. Phys. 64, 467-471, Apr. 1996.