Folium of Descartes
Description
History
This curve is first discussed by Rene Descartes in 1638.
Formula
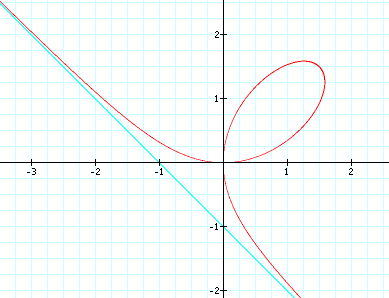
Cartesian: x^3 + y^3 == 3x*y.
Parametric: {3*t, 3t^2}/(1 + t^3). In this formula, the curve tends to the Origin as t→±∞. The curve tends to ∞ when t→-1.
Polar: r==(3*Sin[θ]*Cos[θ])/(Sin[θ]^3+Cos[θ]^3).
Its asymptote is y==x-1.
Properties
