Epicycloid and Hypocycloid

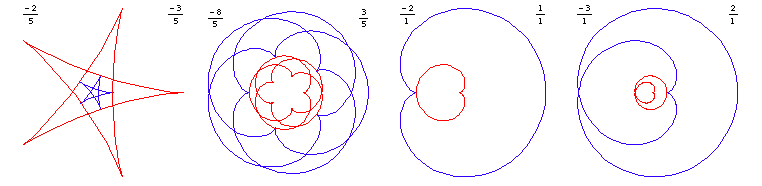
epicycloid hypocycloid gallery — Epicycloid and hypocycloids. The fraction on the upper coners are the two signed parameters b that generates the same curve.

Clear[Epitrochoid, fractionList];
Epitrochoid[a_, b_, h_] := Function[{t},
    {(a + b)*Cos[t] + h*Cos[((a + b)*t)/b],
     (a + b)*Sin[t] + h*Sin[((a + b)*t)/b]}];
fractionList = (Join[-Select[#1, #1 <= 1/2 & ], #1] & )[
   Union[(Join[#1, Range[2, 7]] & )[
     Flatten[Table[p/q, {q, 7}, {p, q*2}]]]]]
GraphicsGrid[(Partition[#1, 5] & )[
   (With[{b = #1, p = Numerator[Abs[#1]],
       q = Denominator[#1]}, ParametricPlot[
       Evaluate[Epitrochoid[1, b, Abs[b]][t]], {t, 0, 2*Pi*p},
       AspectRatio -> Automatic, Axes -> False,
       PlotStyle -> If[b < 0, Red, Blue],
       Prolog -> {If[b < 0, {Text[DisplayForm[FractionBox[-p,
              q]], Scaled[{0, 1}], {-1, 1}],
           Text[DisplayForm[FractionBox[-(q - p), q]],
            Scaled[{1, 1}], {1, 1}]},
          {Text[DisplayForm[FractionBox[p, q]],
            Scaled[{1, 1}], {1, 1}], Text[DisplayForm[
             FractionBox[-(p + q), q]], Scaled[{0, 1}],
            {-1, 1}]}]}]] & ) /@ fractionList]]

epiHypocycloid.nb

History

From Robert Yates:

Cycloidal curves were first conceived by Rømer (a Dane) in 1674 while studying the best form for gear teeth. Galileo and Mersenne had already (1599) discovered the ordinary cycloid. The beautiful double generation theorem of these curves was first noticed by Daniel Bernoulli in 1725. Astronomers find forms of the cycloidal curves in various coronas. They also occur as caustics. The measuring of curve length was given by Newton in his Principia.

Description

Epicycloid is a family of curves.
Epicycloid is a special case of epitrochoid.
Epicycloid is the trace of a point on a circle rolling outside another circle without slipping. (in the same manner a coin rolls around another)

Hypocycloid is a family of curves.
Hypocycloid is a special case of hypotrochoid.
Hypocycloid is the trace of a point on a circle rolling inside another circle without slipping.

When a circle is rolling externally upon a fixed circle we have epicycloid.
When the rolling is internal, we have hypocycloid.
The external and internal rolling can be distinguished as whether the curvature of circles at the point of contact have the same sign. (i.e. if they face the same side.)
From another aspect, if the two circles are situated so that one is inside another, then it's a hypocycloid, otherwise its epicycloid.
Note that when a circle is inside another, the rolling circle can be either the smaller circle or the larger one.

Various sizes of circles generates different epi/hypocycloids.
Let the radius of the fixed circle be a, the radius of the rolling circle be b.
Since the ratio a/b defines the shape of the curve, we will always let a:=1.
Thus epi/hypocycloids are curves of one parameter b.
The parametric formula for both curves can be easily derived from analytic geometry.
It is: {(a + b)*Cos[t] + b*Cos[(a + b)/b*t], (a + b)*Sin[t] + b*Sin[(a + b)/b*t]}
This parametrization has the property that when b is positive, it generate a epicycloid.
When b is negative, it is a hypocycloid.
Thus, a signed parameter b uniquely defines a epi/hypocycloid.

Like epi/hypotrochoids, epi/hypocycloids have the double generation property: for any epi/hypocycloids, there are two unequal signed parameters b1, b2 that gives the same curve. (see Double Generation in the Properties section below.) However, curves that has cusps pointing towards the center are traditionally identified as epicycloids, even though they are also hypocycloids, and curves that has cusps pointing away from center are identified as hypocycloids. We define “n-cusped simple epi/hypocycloid” to be epi/hypocycloids with signed parameter b:=1/+-n. Such curves look like a simple loop, and the curve does not cross itself. They are often just called n-cusped epi/hypocycloid although there are infinity number of epi/hypocycloids with a given number of cusps.

Here are some named cases:

cardioid, b=1 or b=-2
nephroid, b=1/2 or b=-3/2
deltoid, b=-1/3 or b=-2/3
astroid, b=-1/4 or b=-3/4

See Curve Family Index for the family tree of cycloidal curves.

We define the vertexes of the epicycloid to be points on the curve that coincides with a circumscribed circle. Similarly, the vertexes of a hypocycloid are the points on the curve that coincides with a inscribed circle.

Formula

Parametric

Clear[Hypocycloid, Hypotrochoid, Epicycloid, Epitrochoid];

Hypocycloid[n_] := Hypotrochoid[1, 1/n, 1/n];

Hypotrochoid[a_, b_, h_] :=
Function[{t},
 {(a-b) Cos[t] + h Cos[-(a-b)/b t], (a-b) Sin[t] + h Sin[-(a-b)/b t]}
];

Epicycloid[n_] := Epitrochoid[1,1/n,1/n];

Epitrochoid[a_,b_,h_] :=
Function[{t},
 {(a+b) Cos[t] + h Cos[(a+b)/b t], (a+b) Sin[t] + h Sin[(a+b)/b t]}
];

a is the radius of the fixed circle.
b is the radius of the rolling circle.
If b is positive, this formula gives epicycloid.
If b is negative, this formula gives the hypocycloid.
Let a:=1, b:=p/q where p, q are coprime.
Then the formula has a period of 2 Pi*p.
If b is irrational, the formula is nonperiodic.

ParametricPlot[{(a - b)*Cos[t] + h*Cos[-(((a - b)*t)/b)],
       (a - b)*Sin[t] + h*Sin[-(((a - b)*t)/b)]} /.
     {a -> 1, b -> 3/7, h -> 3/7}, {t, 0, 10*Pi}]

derivation

The formula is easily derived using vectors.
Starting with a point on circle a*{Cos[t],Sin[t]}.
Translate that to the center of the rolling circle we have a*{Cos[t],Sin[t]}+b*{Cos[t],Sin[t]}.
Then we need another translation in the direction of the fixed tracing point relative to the rolling circle.
To figure out which direction that is, we need to figure out how many revolutions there are for the rolling circle to go around the fixed circle.
Some thinking and experiment shows it to be (a + b)/b.

Now, suppose the tracing point is fixed h distance on the rolling circle, then we have the formula for general epitrochoid and hypotrochoid

Property. Double Generation

Let the radius of the fixed circle be 1.
The epicycloid with rolling circle radius b is equal to the hypocycloid with rolling circle radius b+1.
This means that every epicycloid can be generated as a hypocycloid.
A hypocycloid can be generated as a epiycloid if and only if its rolling circle is larger than the fixed circle.
For hypocycloid whose rolling circle is smaller than the fixed circle, there are two sizes of the rolling circle that will generate the same curve.
If b1 and b2 are the radiuses of such two rolling circles, then b1+b2==1.

Property. Evolute

The evolute of a epi/hypocycloid is equal to itself.
It is the same as itself scaled and rotated so that the old curve's cusp/vertex coincides with the new curve's vertex/cusp.
The scaling factor is 1/(1+2*b), where b is the signed parameter.

epicycloid nested evolute 34294 nested evolutes a epicycloid

(* plot nested evolute of a epicycloid *)

Clear[n, nestLevel, xrotate, xscale, xcurves, pstyle];

Clear[Hypocycloid, Hypotrochoid, Epicycloid, Epitrochoid];

Hypocycloid[n_] := Hypotrochoid[1, 1/n, 1/n];

Hypotrochoid[a_, b_, h_] :=
Function[{t},
 {(a-b) Cos[t] + h Cos[-(a-b)/b t], (a-b) Sin[t] + h Sin[-(a-b)/b t]}
];

Epicycloid[n_] := Epitrochoid[1,1/n,1/n];

Epitrochoid[a_,b_,h_] :=
Function[{t},
 {(a+b) Cos[t] + h Cos[(a+b)/b t], (a+b) Sin[t] + h Sin[(a+b)/b t]}
];

n = 12;
nestLevel = 10;
xrotate = ((2*Pi)/(n*2));
xscale = (1/(1 - 2/n));

xcurves = Table[ RotationMatrix[xrotate*i] . Epicycloid[n][t] * xscale ^i , {i, 1, nestLevel}]

pstyle = Table[{Hue[0, 1 - i, 0.8], Thickness[.004 + (.008 - .004) i]}, {i, 0, 1, 1/nestLevel}];

ParametricPlot[xcurves, {t, 0, 2 Pi }, PlotStyle -> pstyle, PlotRange -> All, Axes -> False, AspectRatio -> Automatic]

hypocycloid nested evolutes 33dd5 Consecutive evolutes of a hypocycloid.

(* plot nested evolute of a hypocycloid *)

Clear[n, nestLevel, xrotate, xscale, xcurves, pstyle];

Clear[Hypocycloid, Hypotrochoid, Epicycloid, Epitrochoid];

Hypocycloid[n_] := Hypotrochoid[1, 1/n, 1/n];

Hypotrochoid[a_, b_, h_] :=
Function[{t},
 {(a-b) Cos[t] + h Cos[-(a-b)/b t], (a-b) Sin[t] + h Sin[-(a-b)/b t]}
];

Epicycloid[n_] := Epitrochoid[1,1/n,1/n];

Epitrochoid[a_,b_,h_] :=
Function[{t},
 {(a+b) Cos[t] + h Cos[(a+b)/b t], (a+b) Sin[t] + h Sin[(a+b)/b t]}
];

n = 12;
nestLevel = 10;
xrotate = ((2*Pi)/(n*2));
xscale = (1/(1 - 2/n));

xcurves = Table[ RotationMatrix[xrotate*i] . Hypocycloid[n][t] * xscale ^i , {i, 1, nestLevel}]

pstyle = Table[{Hue[.4, 1 - i, 0.8], Thickness[.004 + (.008 - .004) i]}, {i, 0, 1, 1/nestLevel}];

ParametricPlot[xcurves, {t, 0, 2 Pi }, PlotStyle -> pstyle, PlotRange -> All, Axes -> False, AspectRatio -> Automatic]

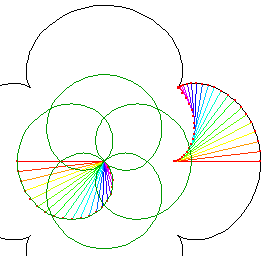
Property. Pedal and Radial

The pedal curve of a epi/hypocycloid (with signed parameter b) with respect to its center is its radial curve scaled (and reflected) by s:=-(1+2*b)^2/(4*b*(1+b)). For epicycloid, the pedal is larger. For hypocycloid, the radial is larger.

Property. Pedal, Radial, and Rose

The pedal of a epi/hypocycloid (with signed parameter b) with respect to its center is equal to the rose r==Cos[1/(-1-2*b)*theta]. The vertexes of epi/hypocycloids coincides with the roses' petal tips. Since pedal of a epi/hypocycloid with respect to its center is equal to its radial, therefore the radial of epi/hypocycloids are also roses.

The following image shows 40 epicycloids (blue) and their pedals (red).

See each of the following page: cardioid, nephroid, deltoid, astroid, for more illustrations of epi/hypocycloid, pedal, and pedal lines.