Envelope

Mathematica Notebook for This Page .

History

From Robert Yates:

Leibnitz (1694) and Taylor (1715) were the first to encounter singular solutions of differential equations. Their geometrical significance was first indicated by Lagrange in 1774. Particular studies were made by Cayley in 1872 and Hill in 1888 and 1918.

Description

Envelope can be thought of as a way of deriving a new curve based on a set of curves. The envelope of a set of curves is a curve C such that C is tangent to every member of the set. (Two curves are tangent to each other iff both curves share a commen tangent at a common point.)

The concept of envelope is easily understood by looking at its graph. When a family of curves are drawn together, their envelope takes shape.

Formula

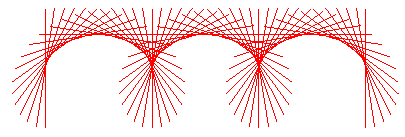
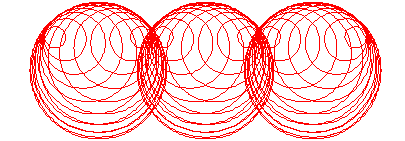
Properties

More examples of envelope can be found in: astroid, cardioid, caustics, deltoid, evolute, lemniscate of Bernoulli, nephroid .

Related Web Sites

See: Websites on Plane Curves, Plane Curves Books .

Robert Yates: Curves and Their Properties .

J W Wilson. Envelopes of Lines and Circles. http://jwilson.coe.uga.edu/Texts.Folder/Envel/envelopes.html