Cardioid
Mathematica Notebook for This Page cardioid_gallery.nb
History
Studied by Ole Roemer (1674) in a investigation for the best form of gear teeth. The name cardioid (heart-shaped; from Greek root cardi, meaning heart) was first used by de Castillon in the Philosophical Transactions of the Royal Society of 1741. Its length is found by Phillipe de la Hire in 1708. Cardioid is a special case of limacon of Pascal: a family of curves studied and named after Étienne Pascal (1588 to 1640), father of Blaise Pascal (1623 to 1662).
Description
Cardioid is a special case of epicycloid and limacon of Pascal. (See: Curve Family Index)
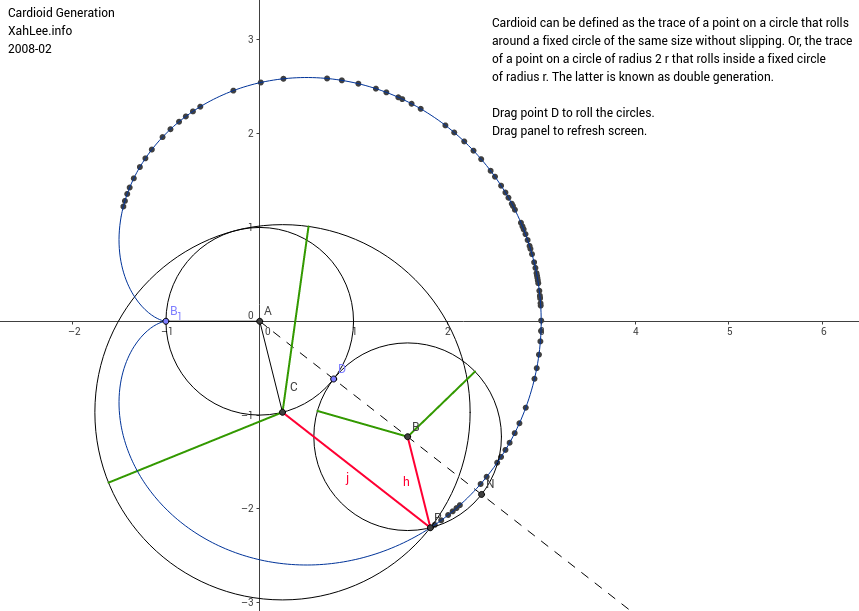
Cardioid can be defined as the trace of a point on a circle that rolls around a fixed circle of the same size without slipping. Or, the trace of a point on a circle of radius 2 r that rolls inside a fixed circle of radius r. The latter is known as double generation. The figure on the right shows the coordination of both generations.
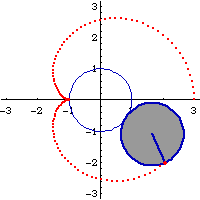
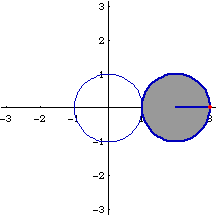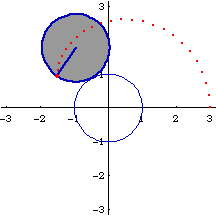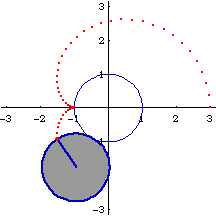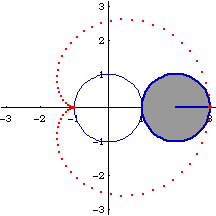
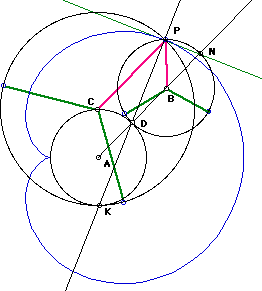
Let A be the center of the fixed circle with radius r. Let B be the center of the rolling circle with radius r. Let P be a arbitrary fixed point on circle B. Suppose P is the tracing point. Let the point of contact of the two circles be D. Let N be a point on the rolling circle that is colinear with ADB. Let K be a point on circle A and colinear with DP. Theorems: PDK is the normal of P. PN is the tangent at P. A circle passing P and K and centered at a point (C) that lies on the fixed circle A will trace out the same cardioid with the tracing point P, by rolling it on the fixed circle with center A. This circle will have radius 2*r.
We define the vertex of a cardioid to be the cusp's opposite point, and the diameter to be the segment from cusp to vertex.
Formula
The following formulas describe a cardioid with cusp at origin and vertex at {4,0}. The a variable is a scaling factor.
- Polar: r==(1 + Cos[θ])*2.
- Polar (flipped along y-axis): r==(1 - Cos[θ])*2*a. θ*3/2==ϕ, and 1/2*θ==ψ. ϕ is the angle of inclination of tangent. ψ is the angle of the radius vector and tangent.
- Cartesian: (-2*x + x^2 + y^2)^2 == (x^2 + y^2)*4.
Properties
Evolute
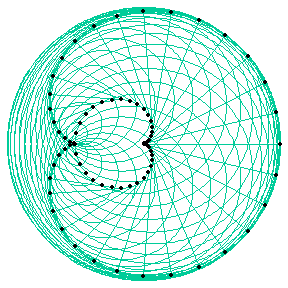
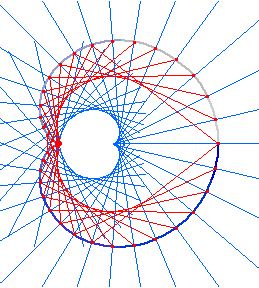
The evolute of a cardioid equals to itself. (true for all epi/hypocycloid) The left figure connects point on the cardioid to their center of osculating circles (green). In the right figure, normals of cardioid are drawn. (the secants shown have no math significance.)
Caustic and Envelope of Circles
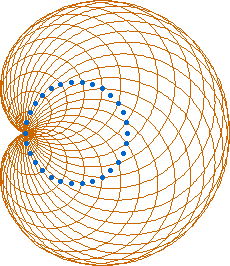
Cardioid is the catacaustic of a circle with light source on the circle. The cardioid so generated is inside the circle with vertex on the point of light source, and has diameter 2/3 of the circle. Cardioid is also the envelope of circles with centers on a fixed base circle C and each circle passing through a fixed point P on the base circle C. The generated cardioid has diameter twice that of C and its cusp is at P.
The catacaustic of a cardioid with lightsource on the cusp is a nephroid.
Pedal and Conchoid of a Circle
Cardioid is the pedal of a circle with respect to a fixed point on the circle. The fixed point forms the cusp of the cardioid, and the circle's diameter is the cardioid's diameter. Cardioid is also the conchoid of a circle of radius r with respect to a fixed point on the circle, and offset 2 r. In others words, any chord of cardioid passing its cusp has constant length 1/2 of the cardioid's diameter, and the locus of midpoints of such chords is a circle. Furthermore, The tangents at the end points of chords passing through the cusp intersects at right angles, and the locus of such intersections is a circle with diameter 3/2 of the cardioid's. Therefore, the orthoptic of a cardioid is a circle.
 Pedal of a Circle |
 Conchoid of a circle |
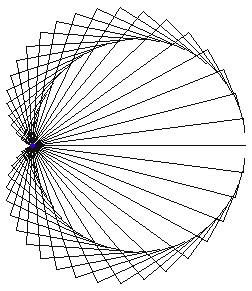
Parallel Tangents
Given any line, there are exactly three tangents parallel to it. If we connect the points of tangency to the cusp, the three segments meet at equal angles of 2*π/3.
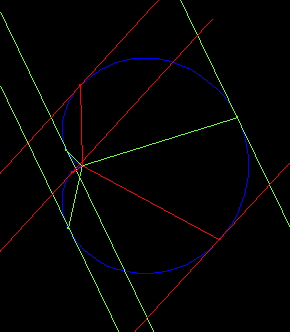
For any line that cuts a cardioid in 4 points, the sum of distances from the cusp to the intersections is equal to the diameter of the cardioid.
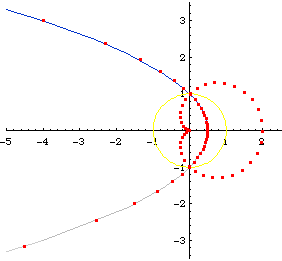
Inverse of Parabola
Cardioid is the inverse of parabola with respect to its focus.
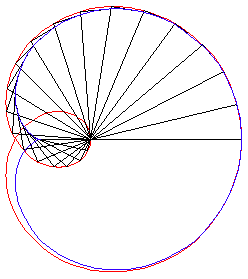
Pedal, Radial, and Rose
The pedal of a cardioid with respect to its center is the a one-petalled rose r==Cos[1/3*θ]. The radial of a cardioid is the same rose. (The pedal and radial of epi/hypocycloids are roses. See each page for the general theorem.)
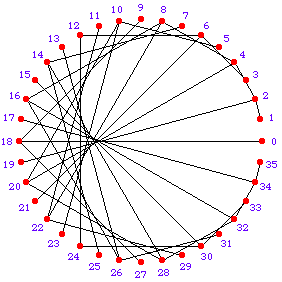
Modular Arithmetic
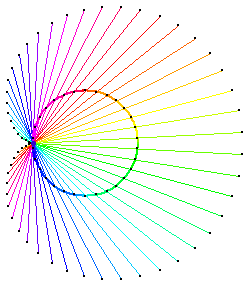
Let there be 36 points labeled 0 to 35 equally spaced on a circle. Connect nth point to Mod[2 n,36] th point. These lines are tangents to a cardioid. it seems that all epicycloids have similar connections to modular arithmetic. Need proof.
Cardioid Graphics Gallery
Limacon of Pascal Graphics Gallery
Why is Mandelbrot Set Cardioid Shaped?
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
- Robert Yates: Curves and Their Properties
- The MacTutor History of Mathematics archive.
- cardioid
- Algebraic Hearts By Ivars Peterson. At http://www.sciencenews.org/view/generic/id/2438/title/Algebraic_Hearts [Science News, Feb. 9, 2002; Vol. 161, No. 6]
- The reflection of light rays in a cup of coffee or the curves obtained with bˆn mod p (1974 to 1979) By Simon Plouffe. At _p/LightsRaysReflections.pdf [mirrored with permission]