Parallel Curve

Mathematica Notebook for This Page parallel_gallery.nb.zip

History

Leibnitz considered parallel curves in 1692-4, following Huygens' (1673) study of involutes.

Description

Parallel are not only defined for lines but for curves as well. Parallel of a curve is the envelope of circles whose centers are on the curve. Alternatively, parallels can be defined as the locus of points Q1, Q2 on the normals of the curve, where Q1 and Q2 are d distant from the curve.

Step by step description:

1. Draw a normal line of length 2 d centerd on a point P on the curve.
2. Repeat this for other points p on the curve.
3. The locus of end points of normal lines are the parallel curves to the given curve with offset d.

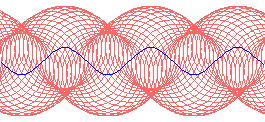
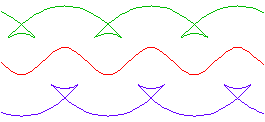
Parallel curves may not be similar to the orginal curve if d is large. Below are three illustrations for the parallels of sine curve. Notice the wedge shaped loop that is not in the original curve.

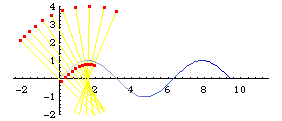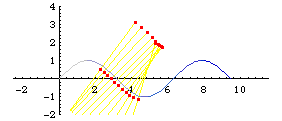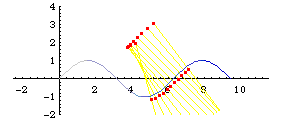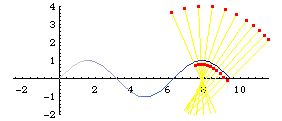
Formulas

Given a parametric curve {xf[t], yf[t]}, the parametric formulas for its parallel (two branches) with a positive offset d is

{ xf[t] + d yf'[t]/Sqrt[xf'[t]^2 + yf'[t]^2], 
  yf[t] - d xf'[t]/Sqrt[xf'[t]^2 + yf'[t]^2] }

This formula is easily derived by considering the unit normal of curve at t, scale it by d, then move it to the point on the curve. If the curve is written in complex notation z[t], then the formula for parallel is simply d*N[t]+z[t], where N[t] is the unit normal at t.

Properties

Parallels and Evolute

Theorem: The locus of Cusps of a curve C's parallel curves is the Evolute of C. This is a alternative definition of evolute.

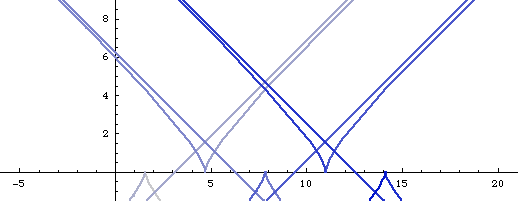
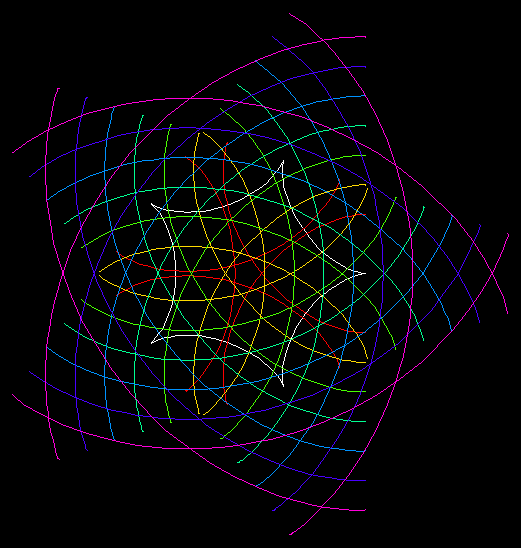
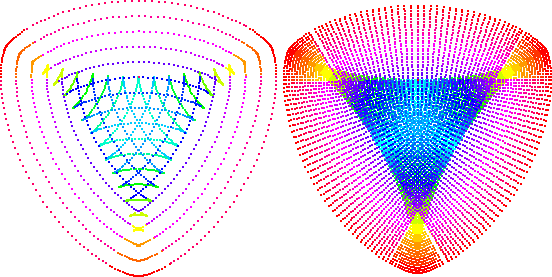
Graphics Gallery

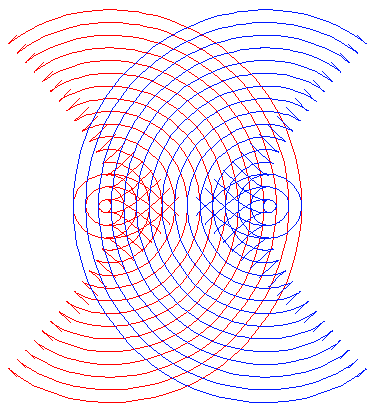
Animation of parallels of a 3-pedaled Rose with varing distance: trifolium_parallel.mov

Related Web Sites

See: Websites on Plane Curves, Printed References On Plane Curves.

Robert Yates: Curves and Their Properties.

Parallel curve.