Cross Curve

Description

Construction of the cross curve:

Let there be a circle centered on the origin. Let P be a point on the circle and O be the origin. Let the intersections of the tangent at P with the x and y axes be M and N. Let a line passing M and perpendicular to x-axis be m. Similarly a line n for N and y-axis. The trace of the intersection of m and n is the Cross Curve, as P moves on the circle.

History

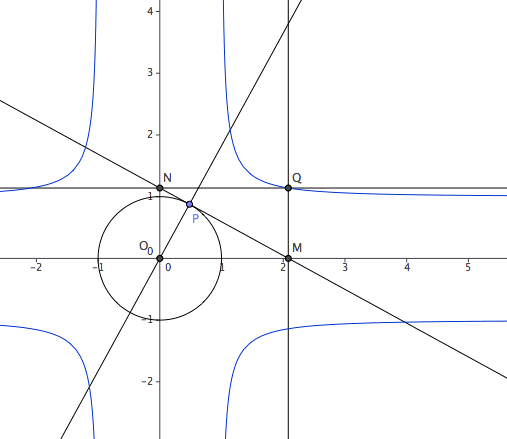
Formula

Start with a circle centered on the origin with radius one {Cos[t],Sin[t]}. Take its tangent vector, then find its tangent equation, then find their intersections with the x and y axes, we easily derive the parametric formula {Sec[t],Csc[t]}. To get the Cartesian equation, we try the art of eliminating a variable. With luck, we use formula Sin[t]^2+Cos[t]^2==1 and fairly easily derive the Cartesian equation x^2+y^2==x^2*y^2.

Note that in deriving the Cartesian equation from the parametric, we have squared both sides of x==Sec[t] and y=Csc[t]. That means, we may obtain extraneous solution when x==0 or y==0, which is the case here. The Cartesian equation x^2+y^2-x^2*y^2==0 has a isolated point {0,0}.

• Parametric: {Sec[t],Csc[t]}.
• Cartesian eq: x^2+y^2-x^2*y^2==0. (has a isolated point at origin.)

Properties