Lemniscate of Bernoulli
Mathematica Notebook for This Page .
History
Studied by Jacob Bernoulli .
Description
Lemniscate of Bernoulli is a special case of Cassinian oval. That is, the locus of points P, such that distance[P,F1] * distance[P,F2] == (distance[F1,F2]/2)^2, where F1, F2 are fixed points called foci. It is analogous to the definition of ellipse, where sum of two distances is replace by product.
Formula
- Parametric: Cos[t]/(1+Sin[t]^2) {1, Sin[t]}, 0 < t ≤ 2 π.
- Polar: r^2 == Cos[2 * θ].
- Cartesian: (x^2 + y^2)^2 == (x^2-y^2).
Foci are at {-1/Sqrt[2],0}, {1/Sqrt[2],0}
Properties
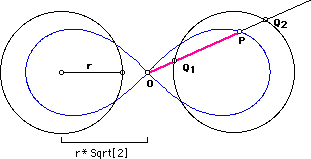
Lemniscate as a Cissoid
Lemniscate of Bernoulli can be generated as a cissoid of two circles.
Step by step description:
- Let there be a circle with radius r.
- Let there be a point O, r*Sqrt[2] distant from the center of the circle.
- Draw a line passing through O and the circle. Let the intersections be Q1, Q2.
- Let there be a vector with origin at O whose length is distance[Q1,Q2].
- The locus of the vector is one loop of the lemniscate of Bernoulli. The other loop is symmetric with respect to O.
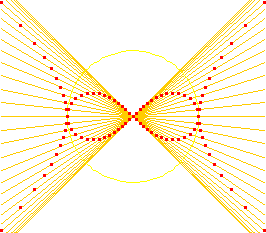
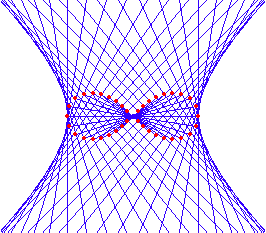
Relation to Rectangular Hyperbola
Its inversion and negative pedal with respect to its center is the rectangular hyperbola. It is also the envelope of circles with centers on a rectangular hyperbola and each circle passing the hyperbola's center.
Slicing a Torus
Lemniscate of Bernoulli is the intersection of a plane tangent to the inner ring of a torus whose inner radius equals to its radius of generating circle. (See: Cassinian oval).
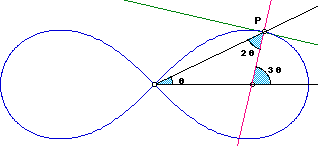
Construction of Tangent and Normal
The normal of any point P on the curve makes a angle 2 theta with the radius vector and 3 theta with the polar axis. The tangent of inclination is 2 theta + π/2.
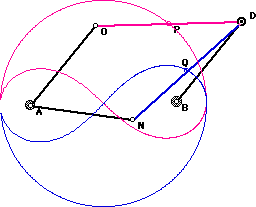
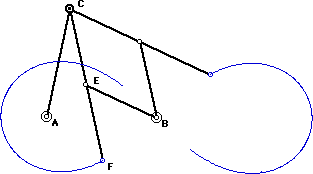
Generation by Linkage
Lemniscate of Bernoulli can be generated by these linkages. On the left: AB == ND == OD == c, AO == AN == BD == c/Sqrt[2]. P and Q are midpoints of line OD and ND respectively. The point P traces half a lemniscate and half a cicle. Same with Q. On the right: AB == AC == a, CE == BE == EF == a/Sqrt[2]
 |
 |
| Lemniscate Linkage 1 | Lemniscate Linkage 2 |
Trivia
The math symbol for infinity is shaped like a lemniscate. It was first used by John Wallis in 1655 in his De Sectionibus conicis (See: A history of mathematical notations By Florian Cajori. Buy at amazon)
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .