Ellipse

History
Description
Ellipse is a family of curves of one parameter. Together with hyperbola and parabola, they make up the conic sections. Ellipse is also a special case of hypotrochoid .
Ellipse is commonly defined as the locus of points P such that the sum of the distances from P to two fixed points F1, F2 (called foci) are constant. That is, distance[P,F1] + distance[P,F2] == 2 a, where a is a positive constant.
The eccentricity of a ellipse, denoted e, is defined as e := c/a, where c is half the distance between foci. Eccentricity is a number that describe the degree of roundness of the ellipse. For any ellipse, 0 ≤ e ≤ 1. The smaller the eccentricy, the rounder the ellipse. If e == 0, it is a circle and F1, F2 are coincident. If e == 1, then it's a line segment, with foci at the two end points.
- major axis is the line segment passing the foci and intersects with the ellipse.
- minor axis is the line segment perpendicular to the major axis, passing the center of foci, and intersects with the ellipse.
- Vertexes is the intersections of the ellipse and the major or minor axis.
- semi major axis is half of the major axis, from center of ellipse to a vertex.
- semi minor axis is half of the minor axis, from center of ellipse to a vertex.
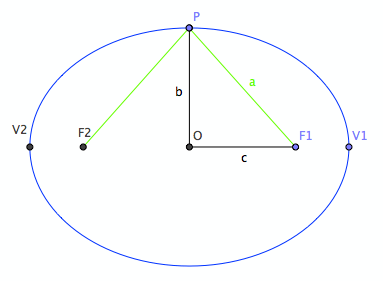
Let a ellipse's sum of distances be “2*a”, and center to a focus be c, and semiminor axis be b, and essentricity be e. These values are related by the formula: b^2+c^2==a^2, e*a==c, and center to a vertex is “a”. This is a very useful formula when trying to solve for a unknown.
Formula
The formula for ellipse can be derived in many ways. By the definition of sum of distances distance[P,F1] + distance[P,F2] == 2*a, setting focuses to be {±c,0} we easily find the Cartesian equation to be:
Sqrt[(x-c)^2+(y-0)^2] + Sqrt[(x- (-c))^2+(y-0)^2] == 2 *a
After getting rid of square roots, we have:
16*a^4 - 16*a^2*c^2 + (-16*a^2 + 16*c^2)*x^2 - 16*a^2*y^2 == 0
which has the form of 2nd degree polynomial. Now minus both sides by a constant we have the form:
x^2/A^2+y^2/B^2==1
for some A and B, where the vertexes of the ellipse happens to be {±A,0} and {±B,0}. To derive the parametric formula, noticed that the x component or y component oscillates. So, if we relpace y by B*Sin[t] and solve for x, we easily found a parametric formula corresponding to x^2/A^2+y^2/B^2==1 to be:
{B* Cos[t], A* Sin[t]}
Similarly, we can derive other forms. The following gives ellipses with eccentricity as parameter, with Vertexes at {±1,0}, and focuses at {±e, 0}.
- Parametric: {Cos[t], Sqrt[1-e^2] Sin[t]}.
- Cartesian: x^2 + y^2/(1 - e^2) == 1
Properties
Point Construction
This method is obvious from the paramteric formula for ellipses {a Cos[t], b Sin[t]}, where a and b are the radiuses of the circles. Figure below showing a ellipse with a:=5, b:=3, and e==8/10.
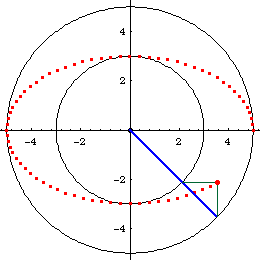
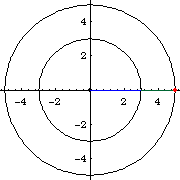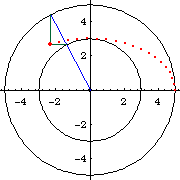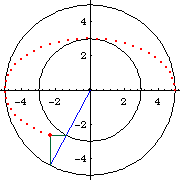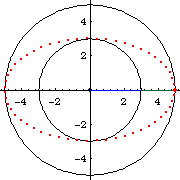
From the point of view of a given ellipse, this is a property that relates a point on the ellipse, to its circumscribed circle, inscribed circle, and center. That is: given a ellipse and a point P on the curve. Let there be lines passing P and perpendicular to the ellipse's major and minor axes. These 2 pendicular lines will intersect the circimscribed and inscribed circles at 2 points, if we consider only intersections that lie in the same quadrant as P. Now, a line, passing these two points will intersect the ellipse's center.
This theorem leads to the Trammel of Archimedes below.
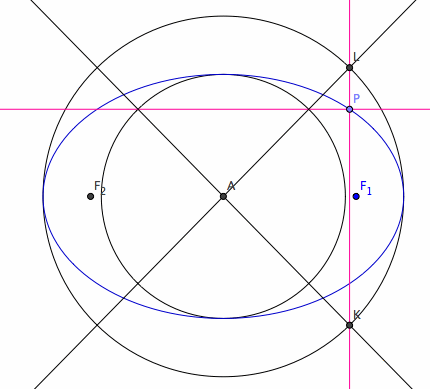
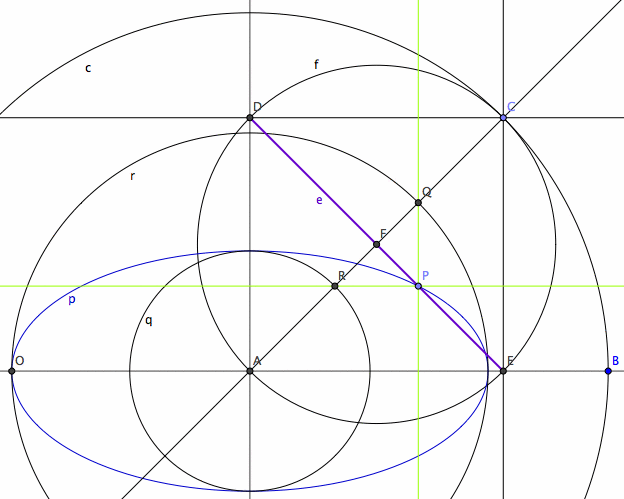
Trammel of Archimedes
Ellipse is the glissette of a line of constant length with endpoints on other two mutually orthogonal lines. That is, the trace of fixed point on a line of constant length with its endpoints freely glides on two mutually orthogonal lines. This mechanism is called Trammel of Archimedes. The trace of the line itself will generate a astroid .
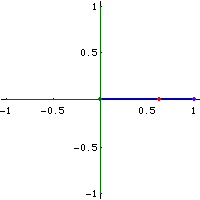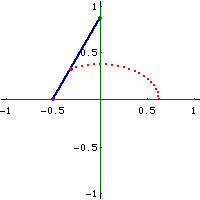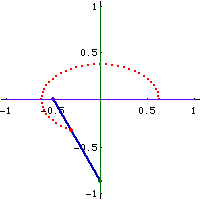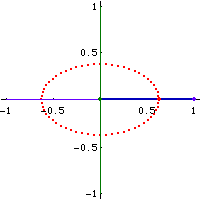
Proof:
- Assume the ellipse to be in a position where its major axis is aligned with the x axis and minor axis aligned with the y axes.
- Let A be the center of ellipse.
- Let P be a point on the ellipse.
- Let there be a circumscribed circle r, and a inscribed circle q.
- Now, let there be a line thru P, parallel to minor axis.
- Let the intersection of this line and the circumscribed circle be Q (pick the intersection that lies in the same quadrant as P).
- Let there be a line thru P, parallel to the major axis.
- Let the intersection of the line and the inscribed circle be R.
- By the point-wise construction theorem, line ARQ are collinear.
- Let F be the midpoint of RQ.
- Let F be the center of a rectangle, and lower left corner at A.
- Label the upper left corner D, upper right C, lower right E.
- Now, consider triangle[Q,P,R].
- Note that dist[Q,R] is constant, angle[Q,P,R]==90°, F bisects QR. Therefore, then distance[F,P] is constant.
- Now, consider the rectangle DCEA. The diagnals of the rectangle is constant, since AF is constant. (AF is constant because F is the bisector of RQ, and R and Q lies on the circum/in-scribed circles, and ARQ is collinear.)
- The distance[D,E] is constant because AC twice of AE, and AE is constant because F is mid of the radiuses of the circumscribed circle and inscribed circle.
- P lies on DE by symmetry arguments with center F.
- (this proof is badly worded and verbose. Exercise: write a better proof)
Tangent Construction
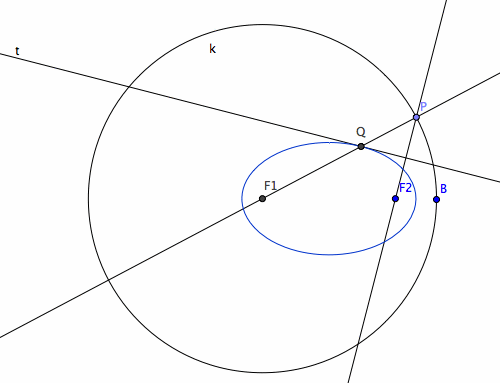
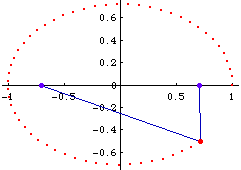
Givens: A circle k with center F1, a point F2 inside the circle, and a point P on the circle. Now, Let t be a line that bisects Line[P,F2]. Let Q be the intersection between t and Line[P,F1]. As P moves around the circle, the traces of Q is a ellipse with focus F1 and F2 and dist[F1,P] being its distance sum, and the line t is its tangent at Q.
Proof: We want to prove that dist[F1,Q]+dist[F2,Q]==dist[F1,P]. Since Q lies on the line t, and t bisects line[P,F2], thus dist[Q,P]==dist[Q,F2]. Since Q also lies on segment[P,F1], so dist[F1,Q] + dist[Q,P] == dist[F1,P]. Combine the above equation together shows dist[F1,Q]+dist[F2,Q]==dist[F1,P]. To show that t is the tangent at Q, note that line perpendicular to t and passing Q bisects the angle[F1,Q,F2]. (detail omitted here)
Note, that the midpoint of P and F2 traces out a circle. This leads to the following theorem that the pedal of a ellipse with respect to a focus is a circle.
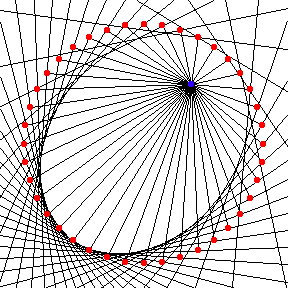
Pedal
The pedal of a ellipse with respect to a focus is a circle, conversely, the negative pedal of a circle with respect to a point inside the circle is a ellipse. This fact can be used to draw ellipses by envelope of lines.
- Start with a circle and a point F1 inside the circle.
- Draw a line j from a point P on the circle to F1.
- Draw a line k perpendicular to j and passing P.
- Repeat step 2 and 3 for other points P on the cricle.
- The envelope of lines m is a ellipse with a focus at F1 and two vertexes touching the circle.
Ellipse as Hypotrochoid
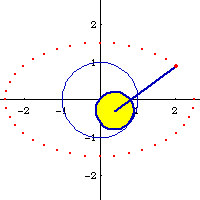
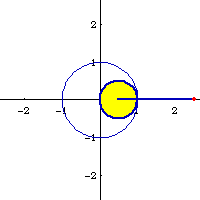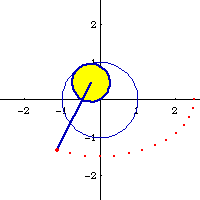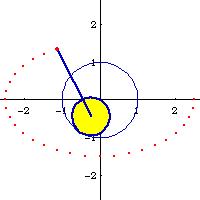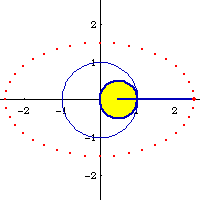
Ellipse can be generated as a hypotrochoid. Let the parameters of the hypotrochoid be {A,B,H}, where A is the radius of the fixed circle, B is the radius of the rolling circle, and H is the distance from the tracing point to the center of the rolling circle. If A/2 == B and H ≠ B, then it's a ellipse with semimajor axis a==B+H and semiminor axis b==Abs[B-H]. Eccentricity is then e:=c/a == Sqrt[a^2-b^2]/a == Sqrt[(B+H)^2-(B-H)^2]/(B+H)
Given A, B:=1/2 A, and e, we may want to find H such that the hypotrochoid {A,B,H} generate a ellipse with eccentricity e. This is easily solved with the above information. The solution is:
h == ( -B (-2+e^2) ± 2 B Sqrt[(1-e)*(1+e)] ) / e^2
If we let A:=1, B:=1/2, e:=8/10, we get h==1/8 or 2. Two ellipses of eccentricity 8/10 as hypotrochoids with parameters {1,1/2,1/8} and {1,1/2,2} are shown below.
Optical Property
Light-rays from one focus will reflect to the other focus. If the radiant point is not at a focus, the envelope of the rays formed is called caustic .


Inversion
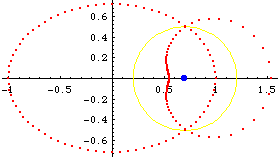
Ellipse's inversion with respect to a focus is a dimpled limacon of Pascal .
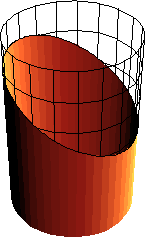
Cylinder Slice
The intersection of a right circular cylinder and a plane is a ellipse. One can see this by tilting a cup or a cone shaped paper cup filled with liquid. Let r be the radius of the base circle of the cylinder, α be the angle formed by the cutting plane and the plane of the base circle of the right circular cylinder. The intersection will be a ellipse with semi-major axis r/Cos[α] and semi-minor axis r.