Orthoptic and Isoptic
Description
A orthoptic of a curve is the locus of all points where the curve's tangents meet at right angles. If the given angle is other than Pi/2, it is called isoptic.
History
Formula
Properties
The orthoptic of a astroid with respect to its center is r^2 == (1/2)*Cos[2*θ]^2. [Robert C Yates.]
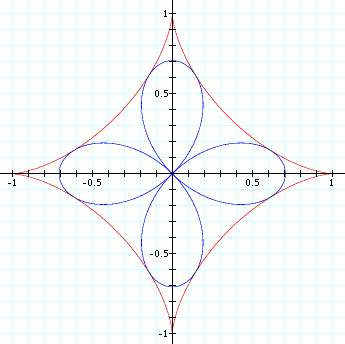
curves relation by Isoptics
| Base Curve | Angle | Isoptic |
|---|---|---|
| parabola | ? | hyperbola |
| parabola | Pi/2 | directrix |
| cardioid | Pi/2 | circle, limacon of Pascal? |
| deltoid | Pi/2 | inscribed circle |
| astroid | Pi/2 | quadrifolium |
| equiangular spiral | Pi/2 | same? equiangular spiral |
| epicycloid | ? | epitrochoid |
| hypocycloid | ? | hypotrochoid |
| sinusoidal spiral | any? | sinusoidal spiral |
| cycloid | ? | curtate or prolate cycloid |
Related Web Sites
See: Websites on Plane Curves, Plane Curves Books .
Robert Yates: Curves and Their Properties .